- · 《建筑材料学报》期刊栏[04/29]
- · 《建筑材料学报》数据库[04/29]
- · 《建筑材料学报》投稿方[04/29]
- · 建筑材料学报版面费是多[04/29]
一、来稿必须是作者独立取得的原创性学术研究成果，来稿的文字复制比（相似度或重复率）必须低于用稿标准，引用部分文字的要在参考文献中注明；署名和作者单位无误，未曾以任何形式用任何文种在国内外公开发表过；未一稿多投。 二、来稿除文中特别加以标注和致谢之外，不侵犯任何版权或损害第三方的任何其他权利。如果20天后未收到本刊的录用通知，可自行处理(双方另有约定的除外)。 三、来稿经审阅通过，编辑部会将修改意见反馈给您，您应在收到通知7天内提交修改稿。作者享有引用和复制该文的权利及著作权法的其它权利。 四、一般来说，4500字（电脑WORD统计，图表另计）以下的文章，不能说清问题，很难保证学术质量，本刊恕不受理。 五、论文格式及要素：标题、作者、工作单位全称(院系处室)、摘要、关键词、正文、注释、参考文献(遵从国家标准：GB\T7714-2005，点击查看参考文献格式示例)、作者简介(100字内)、联系方式(通信地址、邮编、电话、电子信箱)。 六、处理流程：（1） 通过电子邮件将稿件发到我刊唯一投稿信箱（2）我刊初审周期为2－3个工作日，请在投稿3天后查看您的邮箱，收阅我们的审稿回复或用稿通知；若30天内没有收到我们的回复，稿件可自行处理。（3）按用稿通知上的要求办理相关手续后，稿件将进入出版程序。（4） 杂志出刊后，我们会按照您提供的地址免费奉寄样刊。 七、凡向文教资料杂志社投稿者均被视为接受如下声明：（1）稿件必须是作者本人独立完成的，属原创作品（包括翻译），杜绝抄袭行为，严禁学术腐败现象，严格学术不端检测，如发现系抄袭作品并由此引起的一切责任均由作者本人承担，本刊不承担任何民事连带责任。（2）本刊发表的所有文章，除另有说明外，只代表作者本人的观点，不代表本刊观点。由此引发的任何纠纷和争议本刊不受任何牵连。（3）本刊拥有自主编辑权，但仅限于不违背作者原意的技术性调整。如必须进行重大改动的，编辑部有义务告知作者，或由作者授权编辑修改，或提出意见由作者自己修改。（4）作品在《文教资料》发表后，作者同意其电子版同时发布在文教资料杂志社官方网上。（5）作者同意将其拥有的对其论文的汇编权、翻译权、印刷版和电子版的复制权、网络传播权、发行权等权利在世界范围内无限期转让给《文教资料》杂志社。本刊在与国内外文献数据库或检索系统进行交流合作时，不再征询作者意见，并且不再支付稿酬。 九、特别欢迎用电子文档投稿，或邮寄编辑部,勿邮寄私人，以免延误稿件处理时间。
“炒菜式”材料学与“计算”材料学丨科普硅立
作者:网站采编关键词:
摘要：编者按：中科院之声与中国科学院上海硅酸盐研究所联合开设“科普硅立方”专栏，为大家介绍先进无机非金属材料的前世今生。我们将带你——认识晶格，挑战势垒，寻觅暗物质，今
编者按：中科院之声与中国科学院上海硅酸盐研究所联合开设“科普硅立方”专栏，为大家介绍先进无机非金属材料的前世今生。我们将带你——认识晶格，挑战势垒，寻觅暗物质，今古论陶瓷；弥补缺陷，能级跃迁，嫦娥织外衣，溢彩话琉璃。
相信大家对于炒菜一定不陌生，就算自己没亲自炒过，也一定见看过父母、朋友或者是饭店里的厨师炒过。百度百科里面给了“炒菜”相对普适性的的定义:炒菜，是中国菜的常用制作方法，将一种或几种菜在特制的凹型锅内，以火传导到铁锅中的热度为载体，加入油、佐料和菜品后用特制工具“锅铲”翻动将菜炒熟的烹饪过程。
在传统的科学研究中采用的方法往往与“炒菜”模式类似。试验中处理的模型可类比炒菜用的锅，而物理思路和理论分析算法看作是主料，其他各种参数的调节和细节的处理大致就是调料了。在试验中，改变“调料”，改用其他锅或主料，得到的结果也经常不尽相同。但是，这种“炒菜式”的科研方式存在着一个致命的短板，那就是需要消耗大量的人力、资源、时间和金钱，且极大地制约了新材料的发展速度。此时，计算材料学应运而生。
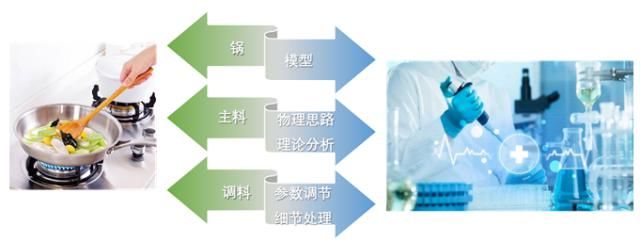图1 炒菜与科研（图片来自网络）
计算材料学是什么？
所谓计算材料学（ComputationalMaterials Science），是一门综合了材料科学与计算机科学且正处于快速发展的新兴学科，是关于材料组成、结构、性能、服役性能的计算机模拟与设计的学科，是材料科学研究里的“计算机实验”。它涉及材料、物理、计算机、数学、化学等多门学科。通俗一点解释为，计算材料学是通过计算机将理论知识编程各种软件程序，然后利用该软件进行一定的科学研究，结合一定的实验数据，快速找出其本质的物理意义，从而完善理论，进一步改善和加速实验研究。
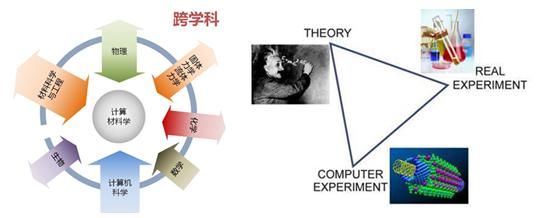图2 计算材料学的构成（图片来自网络）
计算材料学的发展历史
1913年，Niels Bohr建立了原子的量子模型，计算材料学开始萌芽。
1920s~1930s这段时间，由于量子力学的建立和发展，奠定了计算材料学的理论基础。1927年，原子电子结构的Thomas-Fermi理论首先得到运用。1928年，F.Bloch将量子理论运用于固体。在1928-1930三年间，Hatree-Fock方法建立，采用平均场近似求解电子结构的问题。
1946-1965年间，密度泛函理论（DFT）和Kohn-Sham方法从此开启了计算材料学研究的大门。
1998年，Kohn和Pople获得Nobel化学奖。
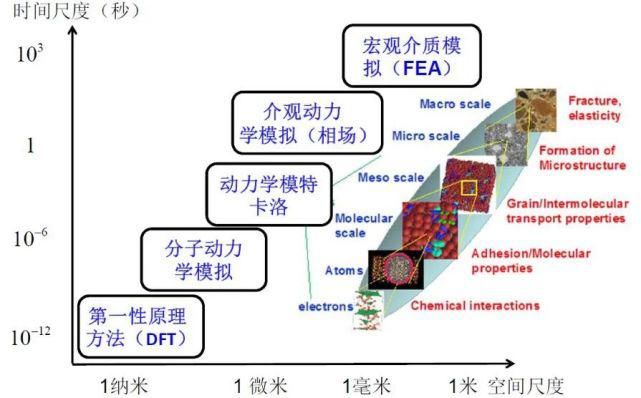图3 计算材料学的研究尺度（图片来自网络）
计算材料学的研究方法
计算材料学可以利用不同的模型和计算方法，从不同尺度与时域研究材料的结构演化及其与性能的相互关系，从而更好地理解和设计新材料。具体的计算方法很多，从空间尺度的不同，分为微观尺度、介观尺度和宏观尺度。
微观尺度（原子尺度及小于晶粒尺寸），利用密度泛函理论（Density Functional Theory, DFT），可以通过电子态密度（Density of Electronic States，DOS）、巴德电荷（BaderCharge）以及局域电荷密度等很好地将电子信息与材料性能和结构联系在一起。另外，也可以选择分子动力学（Molecular Dynamics，MD）和蒙特卡罗方法（MonteCarlo, MC）来寻找原子的迁移路径和势垒。针对具有十分复杂的界面结构的问题时，用经典尖锐界面模型去跟踪界面演化，会遭遇到严重的数值困难。并且真实材料中的相界或晶界实际上并不是严格的零厚度界面，而是具有一定厚度（纳米尺度）的边界层，这层厚度控制材料相变动力学，由此引入一个序参量场区分两相（如固相和液相），该方法为相场法（Phase-field method, PFM），相场法被广泛应用于模拟液/固相变（枝晶生长、多元多相凝固、多晶凝固等）、固态相变（沉淀相析出、马氏体相变、铁电相变等）、应力相变（薄膜生长，定向粗化）、结构缺陷相变（裂纹扩展、位错动力学）等。在微观尺度内，还有微观动力学模拟等方法。
介观尺度（晶粒尺寸大小），主要有元胞自动机法，以晶粒生长为例，元胞自动机的模拟过程主要有确定形核、选择时间步长、计算温度场、计算溶质场、计算界面元胞的生长动力学、确定胞状态、捕捉邻胞、计算曲率等过程组成。
宏观尺度（宏观试样大小），主要是有限元分析(Finite Element Analysis, FEA)方法，该方法是利用数学近似的方法对真实物理系统进行模拟，还利用简单而又互相作用的元素就可以用有限数量的未知量去逼近无限未知量的真实系统。
文章来源：《建筑材料学报》 网址: http://www.jzclxb.cn/zonghexinwen/2021/0507/362.html